Correlation - Is our portfolio well diversified?

In probability theory and statistics, correlation (often measured as a correlation coefficient) indicates the strength and direction of a linear relationship between two random variables [1].

We can use correlation to evaluate how our stocks are prone to move together.

A well differentiated portfolio should have stocks that do not behave the same over time. Every day we should own stocks that win and stocks that lose (ideally more of the former and les of the latter) so that on average we gain more than the market in good times and lose less than the market in bad times.

Two stocks are perfectly correlated if there is a linear relation between them. Let's suppose to own stock A and stock B. If stock B gains X% everytime stock A gains X%, and stock B loses X% everytime stock A loses X%, then stock A and stock B have a correlation factor of 1. The same if stock B gains/loses 2, 3, 4 or n times X%. There is a linear dependency between the two stocks price.

Let's take as an example some of our stocks, starting from ADBE and FLS.

If we represent on a chart the prices of ADBE and FLS as points over one year (axys X is ADBE price and axys Y is FLS price) we see that these points lay on a sort of a line. Correlation for ADBE and FLS is 91%, meaning that they move in a very similar way. ADBE goes up, then FLS goes up too.

Let's look now at the correlation between AFAM and DECK.

In this case a linear pattern cannot be identifies. In fact the correlation factor in this case is around 7%.

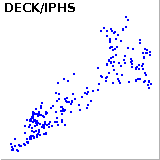
As a further example let's have a look at the correlation between IPHS and some other of our stocks:

If we consider all the correlation factors in our portfolio we get an average correlation of 62%.

From sone research I did it seems like a good portfolio mix has a correlation between -80% and 80%. But, of course, I would like to read your comments on this.

[1] http://en.wikipedia.org/wiki/Correlation